A-3

$ \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} $

整数の性質（Number Thorem）

1 約数と倍数

1.1 約数と倍数

使えるコマンドを使ってみる。

$$問１　ab+3a+2b=1 をみたす整数の組 (a,b) を求めよ。$$

もちろん，整数論では，文字の部分を因数分解して，
\[(a+2)(b+3)=7=-7\cdot(-1)=-7\cdot(-1)=1\cdot 7=7 \cdot 1\] \[(a+2,b+3)=(-7,-1),(-1,-7),(1,7),(7,1)\] \[(a,b)=(-9,-4),(-3,-10),(-1,4),(5,-2)\] \[しかし，関数的に解けば，b=-3+\frac{7}{a+2}\] \[a+2 が7の約数 -7,-1,1,7 で解決\] さらに,グラフで言えば，グラフが格子点を通るところを探せばいい。
\[対称性により，aが-1以上5以下を調べればいい。\]
さて，Pythonでプログラミングしてみよう。
#2元2次不定方程式の整数解

import sympy

def futei2(a,b,c):
　　l=sympy.divisors(a*b-c)
　　for i in range(0,len(l)):
　　　　x=l[i]-b
　　　　y=int(-a+(a*b-c)/(x+b))
　　　　print("(",x,",",y,")")
　　for i in range(0,len(l)):
　　　　x=-l[i]-b
　　　　y=int(-a+(a*b-c)/(x+b))
　　　　print("(",x,",",y,")")

futei2(3,2,-1)

( -1 , 4 )
( 5 , -2 )
( -3 , -10 )
( -9 , -4 )

1.2 最大公約数と最小公倍数

問２　最大公約数が15，最小公倍数が180である2つの自然数の組をすべて求めよ。

これ，Geogebra向きじゃないな・・というときに「Python」，
と言っても，下のMaximaでやったのを，Pythonに変えただけだけど。
しかも，ただ調べてるだけ。答えあってるかどうかに使う。

#最大公約数 g,最小公倍数 l の2数
def glc(g,l):
　　for i in range(g,l+1):（これ for i=1 to lの意味）
　　　　for j in range(i,l+1):
　　　　　　if gcd(i,j)==g and lcm(i,j)==l:
　　　　　　　　print("(",i,",",j,")")
glc(15,180)とやると
( 15 , 180 )
( 45 , 60 )

1.3 整数の割り算と商および余り

2 ユークリッドの互除法

2.1 ユークリッドの互除法

TeXをやっている人に，emathのマクロを使って，互除法を計算させる方法がある。

TeXのソースに$\Gozyohou{321}{123}$と書くだけで，すべて自動でやってくれるんですよ。
もちろん，emathをusepackageするんですけど。詳しくは「emath」

2.2 1次不定方程式

下の進法と図の格子点
\[163x+78y=1の整数解\]

整数解の特殊解(-11,23)を求めるのは，教科書は互除法使用。

これ以上長くなると，この方法だと苦しい。
2つの違う方法を紹介しよう。

その１　合同法
\[163x\equiv 1(\mod 78)\cdots ①　（163\equiv 7(\mod 78)より）\] \[7x\equiv 1(\mod 78)\cdots ②\] \[161x\equiv 23(\mod 78)\cdots ②\times 23\] \[2x\equiv -22(\mod 78)\cdots ③　　①-②\] \[6x\equiv -66(\mod 78)\cdots ④　③\times 3\] \[x\equiv 67(\mod 78)　②-④\] \[x\equiv -11(\mod 78)　（67\equiv -1(\mod 78)より）\] その２　連分数使用
\[\frac{163}{78}=2+\frac{1}{11+\frac{1}{7}}\] 最後の1個前までの連分数を直して $2+\frac{1}{11}=\frac{23}{11}$
これで解けてるんだから，これが一番いいじゃないの？
pythonで求めよう。

import math
from fractions import Fraction

def dio(a):
　　l=[]
　　while a-math.floor(a)>0.001:
　　　　b=math.floor(a)
　　　　l.append(b)
　　　　a=1/(a-b)
　　a=Fraction(0,1)
　　for i in range(0,len(l)):
　　　　a=1/(a+Fraction(l[len(l)-i-1]))
　　print("x="-,a.denominator,"y=",a.numerator)

dio(163/78)

x=- 11 y= 23

連分数を使った方法です
詳しくは「再読　高木貞治」の「初等整数論講義」（＊）

3 整数の性質の活用

3.1 ｎ進法

これもemathの紹介。

\usepackage{emNsinhou}として
\dectoN_{3}{23}\foo
$\foo_{(3)}$
\showdectoN

3.2 分数と小数

実数の所で記述。

整数の性質（Number Thorem）

1 約数と倍数

1.1 約数と倍数

新教育課程の整数論は,私の「再読　高木貞治」の「初等整数論講義」（＊）の簡易版という感じだ。
Maxima でおっていこうか。

すべての約数を見るのは divisors()
すべての約数の和は divsum()
だから　約数の個数は cardinate(divisors())

倍数の見分け方がある
もちろん,7はない。知りたい人は＊をどうぞ。

素数 prime ラテン語「第一の」の意から
合成数 composition 古期フランス語「共に置く」の意から_
因数 factor
素因数
素因数分解 factorization

素因数分解は factor()
素数とその指数を見る ifactors()

(%i1)

divisors(28);

\[(\%o1) {1,2,4,7,14,28}\]

(%i2)

cardinality(divisors(28));

\[(\%o2) 6\]

(%i3)

divsum(28);

\[(\%o3) 56\]

(%i4)

factor(28);

\[(\%o4) {{2}^{2}}7\]

(%i5)

ifactors(28);

\[(\%o5) [[2,2],[7,1]]\]

この応用として２元２次不定方程式がある。
$$問１　ab+3a+2b=1 をみたす整数の組 (a,b) を求めよ。$$
２元２次方程式を解くプログラムを一応作ったがこれじゃあなあ,まあ,もっと研究しよう。

(%i6)

for a:-50 thru 50 do
for b:-50 thru 50 do
if a*b+3*a+2*b=1 then print("(",a,",",b,")")$

\[( -9 , -4 ) ( -3 , -10 ) ( -1 , 4 ) ( 5 , -2 ) \] もっといい奴を

und(a,b,c):=block(
l:listify(divisors(a·b−c)),
l:join(l,−l),
for i:1 thru length(l)do(
　　x:l[i]−b,
　　y:−a+(a·b−c)/(x+b),
　　print("(",x,",",y,")")
　　)
);

und(3,2,−1);
\[( -9 , -4 ) ( -3 , -10 ) ( -1 , 4 ) ( 5 , -2 ) \]

1.2 最大公約数と最小公倍数

(%i8)

gcd(12,45);lcm(12,45);

\[(\%o7) 3\] \[(\%o8) 180\]

問２　最大公約数が15，最小公倍数が180である2つの自然数の組をすべて求めよ。
いろいろ考えるより調べてしまえというマクロ

(%i9)

glc(g,l):=block(
   for i:g thru l do
   for j:i thru l do
   if gcd(i,j)=g and lcm(i,j)=l then print("(",i,",",j,")")
)$

(%i10)

glc(15,180)$

\[( 15 , 180 ) ( 45 , 60 ) \]

1.3 整数の割り算と商および余り

割り算の商は floor(a/b)床関数　あるいは　quotient(a,b)
　a/bが負に注意
余りは mod(a,b)
両方一気に出すのは divide（a,b）ただし，下のように注意が必要

(%i11)

floor(-29/7);

\[(\%o11) -5\]

(%i12)

quotient(-29,7);

\[(\%o12) -4\]

(%i13)

mod(-29,7);

\[(\%o13) 6\]

(%i14)

divide(-29,7);

\[(\%o14) [-4,-1]\]

(%i15)

divide(29,7);

\[(\%o15) [4,1]\] すべての自然数の平方は4で割った余りが0か1を実験

(%i16)

l:[0,1,2,3]$

(%i17)

mod(l^2,4);

\[(\%o17) [0,1,0,1]\] n(n+1)(2n+1)　は6の倍数であることの実験

(%i18)

l:[0,1,2,3,4,5]$

(%i19)

mod(l*(l+1)*(2*l+1),6);

\[(\%o19) [0,0,0,0,0,0]\]

2 ユークリッドの互除法

2.1 ユークリッドの互除法

2.2 1次不定方程式

そして２元１次方程式（ディオファンタス方程式）
特殊解を見つけて一般解にするというもの,特殊解が見つけずらいものは互除法を使うという流れだ。
図形的な意味もある,詳しくは＊。
ディオファンタス方程式を解くには,ユークリッドの互除法を使う方法と,合同式を使う方法と,連分数を使う方法がある。詳しくは＊。
上は合同法を使った解法，下は連分数を使った解法，連分法のほうがいいのかな。

(%i20)

dio(a,b):=block(
x:inv_mod(a,b),
y:(1-a*x)/b,
return([x,y])
)$

(%i21)

dio(163,78);

\[(\%o21) [67,-140]\]

(%i22)

diof(a,b):=block(
r:radcan(cfdisrep(delete(last(cf(a/b)),cf(a/b)))),
return([-denom(r),num(r)])
)$

(%i23)

diof(163,78);

\[(\%o23) [-11,23]\]

3 整数の性質の活用

3.1 ｎ進法

Maximaには ibase（input base）とobase（output base）なる変数がある。
もちろんデフォルトは10。
ただし整数のみ，しかも環境変数みたいなもので直さないといけない。

(%i24)

ibase:2$

(%i25)

10101;

\[(\%o25) 21\]

(%i26)

ibase:1010$

(%i27)

obase:2$

(%i11100)

67;

\[(\%o11100) 1000011\]

(%i11101)

obase:10$

以下ぎこちないが，p進法に直す，p進表示を十進法に直すマクロ。

(%i30)

nota(a,p):=block(
l:[ ],
for i:1 while i<100 do
(
l:append([mod(a,p)],l),
a:floor(a/p),
if a=0 then return(l)
)
)$

(%i31)

nota(23,3);

\[(\%o31) [2,1,2]\]

(%i32)

nota10(l,p):=block(
s:0,
(
for i:0 thru length(l)-1 do
s:s+l[length(l)-i]*p^i
),
return(s)
)$

(%i33)

nota10([2,1,2],3);

\[(\%o33) 23\]

小数入りのマクロ
　2進数で1.111だったら，nota11([1,2,1,1,1],2)と入力。
10進小数をp進法に直すのは，すぐ無限になりそうなのでやめとこ。

(%i34)

nota11(l,p):=block(
s:0,
(
for i:1 thru length(l) do
if l[i]=p then k:i
),
(
for i:1 thru k-1 do
s:s+l[i]*p^(k-i-1)
),
(
for i:k+1 thru length(l) do
s:s+l[i]*p^(-i+k)
),
return(float(s))
)$

(%i35)

nota11([1,2,1,1,1],2);

\[(\%o35) 1.875\]

3.2 分数と小数

循環小数 recurring decimal
　循環といえばFermatの小定理，オイラーの定理までやりたいところだが。
　連分数まで入試問題には出ていたりする。
＊を参照していただければ。
循環小数を分数に直すマクロです。
例えば 0.1272727...ならば

(%i36)

recurde(a,b):=block(
r:-floor((log(b))/(log(10))+1),
return(a*b/(1-10^r)/10^(-r-1))
)$

(%i37)

1/10+recurde(1/100,27);

\[(\%o37) \frac{7}{55}\]

整数の性質（Number Thorem）

1 約数と倍数

1.1 約数と倍数

整数 integral number,integer アンタッチャブル：完全という意味あり、整数と積分は完全なのだ。
正の整数 positive ラテン語「(協定で)決まった」の意から
自然数数の世界はここからスタート
負の整数 negative 「否定する」まさに否定された数
　たまに，負の数と負の数を掛けるとどうして正になるのか，と質問する生徒がいる。
　証明を聞きたいんじゃなくて，自分なりに納得したいんだよなきっと。
割り切れる divisible （divide ラテン語「分離する」の意から）
約数 divisor,factor（ラテン語「作る[なす]人」の意から）
倍数 multiple（ multi-「多くの…」）

1.2 最大公約数と最小公倍数

最大公約数 great common divisor(measure)
最小公倍数 least common multiple
互いに素 co-prime
2数の関係 ab=gl があり,これを使った問題がある。

1.3 整数の割り算と商および余り

商　quotient
余り　remainder
剰余類　residue class
　整数を余りで分類する方法
合同の記号は教科書では発展にある。

2 ユークリッドの互除法

2.1 ユークリッドの互除法

ユークリッドの互除法で最大公約数を求める。
ユークリッドの互除法は昔の書き方があるが，教科書はそれを採用していない。
この方法の書き方を提言する。
図１がいいと思うが，図２が昔の書き方

図 1:

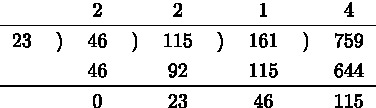
図 2:

2.2 1次不定方程式

そして２元１次方程式（ディオファンタス方程式）
特殊解を見つけて一般解にするというもの,特殊解が見つけずらいものは互除法を使うという流れだ。
図形的な意味もある,詳しくは＊。
ディオファンタス方程式を解くには,ユークリッドの互除法を使う方法と,合同式を使う方法と,連分数を使う方法がある。詳しくは＊。

3 整数の性質の活用

3.1 ｎ進法

p進法 notation

これも，部分分数分解などの応用があり，詳しくは＊

3.2 分数と小数

循環小数 recurring decimal
　循環といえばFermatの小定理，オイラーの定理までやりたいところだが。
　連分数まで入試問題には出ていたりする。
＊を参照していただければ。

Created with wxMaxima.